Un commentaire récent sur le premier article consacré au rectangle harmonieux, m’a donné envie de faire à nouveau quelques recherches …

Voici un passage, consacré à l’emploi des consonances musicales, tiré de « La géométrie secrète des peintres », un ouvrage complexe mais passionnant dont je lis les chapitres à doses homéopathiques 🙂

Harmonie…musicale !! Encore des mathématiques : oui, mais…

Comme au Moyen Âge on les rattache à Pythagore à travers le Timée de Platon, et on cherche en elles le sens secret de l’univers ; mais leur connaissance est devenue beaucoup plus précise ; et surtout il ne s’agit pas des mêmes mathématiques.
Au Moyen Âge, toutes les recherches se faisaient à la pointe du compas. Cela permettait l’emploi courant des quantités incommensurables, et en particulier, de la proportion d’or : travail de géométrie pratique, conforme à des procédés, à des trucs d’atelier qu’embellissait une mystique, mais travail d’artisan malgré tout. La génération de l’humanisme (dont Leon Battista Alberti pour l’architecture et Piero della Francesca pour la peinture) se plonge au contraire dans les livres. […]
Le résultat, c’est d’abord la précision, les idées claires, les calculs exacts sur les nombres ; et par là une désaffection grandissante pour les tracés au compas qu’on ne peut calculer, tandis que croît le goût des rapports simples et mesurables : c’est le désir de rattacher les arts plastiques à l’art majeur qu’est la musique par l’emploi des rapports musicaux. […]

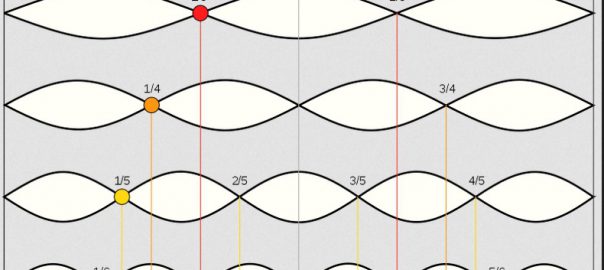
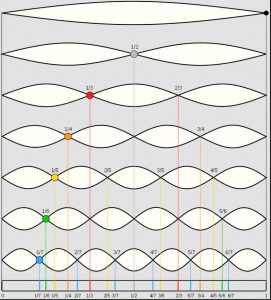
 Alberti explique que les intervalles musicaux agréables à l’oreille, l’octave, la quinte et la quarte correspondent à la division d’une corde en 2, en 3 ou en 4 (1/2, 2/3, 3/4). Ces proportions qu’on appelle à l’époque diapason, diapente, et diatessaron, serviront aussi de base aux arts plastiques, et d’abord à l’architecture. […]

Nous sommes bien loin de l’ouvrage de Pacioli où était glorifiée une certaine proportion appelée « divine » justement parce qu’elle était incommensurable. Ici, la beauté réside dans les rapports des premiers nombres entiers, rapports simples, faciles à lire d’un coup d’œil, et toujours mesurables. Non pas n’importe quels rapports, il est vrai, mais seulement ceux qui se trouvent dans l’échelle musicale : l’esthétique qui en résulte est nettement différente de celle de Pacioli même si l’attitude intellectuelle reste encore imprégnée de cette grande quête métaphysique qui faisait la noblesse du Moyen Âge. […]
Cette musique, c’est un miracle qu’elle se soit concrétisée et qu’elle se dégage avec tant de grâce et de pureté des monuments qu’Alberti a construit comme de toutes les œuvres des architectes, des peintres et des sculpteurs qui se sont pénétrés de ses idées. […]

« Leonard de Vinci, passionné de musique parle avec beaucoup de subtilité des rapports de l’art des sons avec la peinture mais sa manière de concevoir ces rapports est certainement personnelle. »

À partir de quelques exemples , j’ai tracé ci-dessous les différentes césures : les explications sont issues de l’ouvrage.

Benozzo Gozzoli : Cortège des mages

Rapport 2/3/4
« Division de l’octave 1/2 en quinte et quarte 2/3 et 3/4.
B est au 2/3 de AC et C au 3/4 de AD. « Ce sont les grands arbres qui scandent cette musique plastique. »

Le Titien : Bacchus et Ariane

Rapport 4/6/9
« Bacchus est sur la césure 4 en partant de la gauche. La même césure en partant du haut, établit la taille des personnages.
La césure verticale 6 assure la mise en place du tronc de l’arbre.
– l’oblique ED partant de cette coupure 6 sur le côté supérieur et rejoignant l’angle inférieur droit du rectangle est le thyrse du personnage de droite ;
– l’oblique FC partant du haut de la césure 4 vers l’angle inférieur gauche commande la jambe d’Ariane et son mouvement de marche.
– l’oblique BG qui part du sommet supérieur droit et rejoint la césure 6 à gauche donne à Bacchus son envolée vers Ariane et à celle-ci son mouvement de crainte. »

Mantegna : Le Parnasse

Rapport 9/12/16
« Dans cette expression achevée de l’humanisme, l’emploi des rapports musicaux platoniciens s’imposait. Mantegna se plie ici aux exigences du double diatessaron.
La césure 9 en partant de la droite est celle qui axe le tableau : en haut elle situe Mars et Vénus, en bas elle oriente le mouvement des jambes des Muses.
Le même rapport est pris en partant de la gauche ce qui permet l’établissement d’obliques. (non représentées sur mon croquis) Mantegna pousse le symbolisme très loin : il dispose déjà des 9 Muses, il présentera en tout 16 personnages. »

« Les artistes de la Renaissance ont pris à la lettre le texte d’Alberti, s’appuyant de préférence sur les nombres que celui-ci proposait à titre d’exemple, et les rappelant même dans leurs figurations. Les « aires » moyennes convenaient particulièrement aux peintres qui se sont donc spécialement intéressés aux rapports 4/6/9 et 9/12/16.« 

« Ces proportions peuvent être doublées, ou combinées,sans toutefois dépasser le nombre 27, le troisième cube,car les Anciens ont remarqué que les lois mathématiques de la musique n’étaient valables que pour les petits nombres. »

Edit du 20/12/2019

Correspondance entre les nombres et les sons :
-la corde divisée en 2 fait vibrer la moitié de celle-ci, le son obtenu est plus aigu d’une octave que le son initial
-même expérience avec les 2/3 de la corde puis les 3/4 le son initial plus haut d’une quinte puis d’une quarte.

L’ intervalle entre deux notes est le rapport de la fréquence  de chacune.
La note fondamentale (ou note de base) sur laquelle est construit un accord.
Les accords se construisent à partir d’intervalles .

Combinaison d’intervalles :
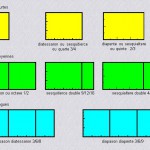
Octave 2/1 = 2
Quinte 3/2  
Tierce 5/4
les autres intervalles en découlent soit :
–> Quarte = octave-quinte
Ton majeur = la quinte-la quarte (9/8)

L’addition de 2 intervalles s’obtient en multipliant leurs rapports, par exemple :
la quinte +la quarte–> 3/2 x 4/3 = 2/1 soit 2 (l’octave)
La soustraction de 2 intervalles s’obtient en divisant leurs rapports, par exemple :
l’octave – la quinte–> 2/1:3/2 = 4/3 (la quarte)

Les rapports harmoniques et complémentaires :

« L’octave. C’est le rapport le plus simple qui soit : celui qui lie une fréquence fondamentale à sa première harmonique ! Ce rapport est de 2.

En partant d’une fréquence de 250 Hz par exemple, la fréquence suivante séparée d’une octave sera 500 Hz, puis 1000 Hz, puis 2000 Hz, 4000 Hz, etc…

Quand n2 est à l’octave de n1 (lorsque n2 = 2 x n1), tous les harmoniques de n2, et n2 lui-même, sont des harmoniques de n1 ! D’une certaine façon, n2 disparaît dans n1.
C’est un phénomène extrêmement repérable, et que toutes les cultures de notre planète ont observé et intégré à leurs langages musicaux. C’est la raison pour laquelle l’octave été choisie pour servir d’échelle et structurer nos gammes.
Quand un homme et une femme chantent ensemble, ils vont généralement chanter à une ou plusieurs octaves de distance, sans le chercher, et sans même souvent en prendre conscience, tant cela leur semblera naturel.

Dans toute la suite de ce dossier et par souci de simplification, on représentera une octave par l’intervalle [1 ; 2] (et non plus [250 ; 500] comme au dessus). Car finalement, la borne de départ n’a que très peu d’importance. Personne ne sais d’ailleurs comment la fréquence du Do (première note de notre échelle musicale) a été choisie. Cela aurait pu être n’importe quelle fréquence, cela n’aurait rien changé…
Comme nous l’avons vu ce qui importe, c’est le rapport entre les notes. Et l’avantage de commencer par 1 est justement que la fréquence d’une note correspondra à son intervalle / son rapport avec notre note de référence (car la division se fera par 1) ! »  Source

« Wittkower a mis en lumière la raison profonde de ce goût des rapports simples et mesurables : c’est le désir de rattacher les arts plastiques à l’art majeur qu’est la musique, par l’emploi des rapports musicaux. » (extrait de La géométrie secrète des peintres)

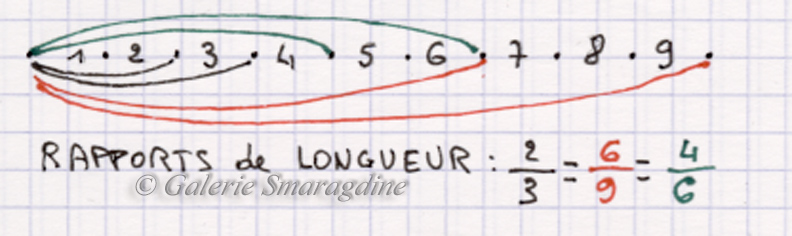
« Alberti a une manière particulière d’établir ses rapports : il part de la plus petite mesure (ci-dessous intervalle 4) qui se trouvera aux 2/3 de l’intervalle 6 ; la longueur 6 est aux 2/3 de 9. »

On peut encore prolonger en partant de l’intervalle 9 en reportant 2 fois 3/4